INDICE
Polígonos
Elementos y propiedades:
-Ángulos central
-Ángulo interior
-Suma de ángulos centrales, ángulos interiores y exteriores
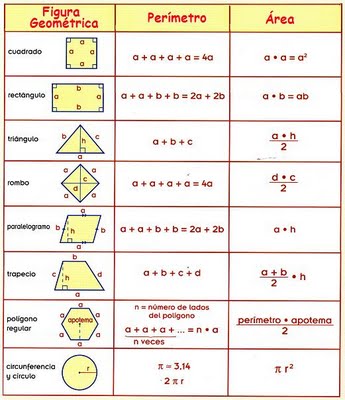
-Perímetro y área de polígonos regulares e irregulares
-Circunferencia
-Rectas y segmentos
-Ángulo
-Circunferencia
-Rectas y segmentos
-Ángulo
-------------------------------------------
Polígonos
"polígono" proviene de la raíz poli (muchos) y gono(ángulos), es decir muchos ángulos. Es una figura compuesta por una secuencia finita de segmentos rectos que encierran una región formando una figura plana, éstas figuras tienen su nombre según el numero de lados

Es requisito geométrico que dos lados que se intersecan en un vértice formen un ángulo no llano (distinto a 180°), ya que de otra manera los segmentos se considerarían partes de un lado único; sin embargo, esos vértices podrían permitirse algunas veces.

En un polígono se pueden distinguir los siguientes elementos geométricos:
*Lado (L): es cada uno de los segmentos que conforman el polígono.
*Vértice (V): es el punto de intersección (punto de unión) de dos lados consecutivos.
*Diagonal (d): es el segmento que une dos vértices no consecutivos.
*Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
*Semiperímetro (SP): es la mitad del perímetro.

*Ángulo interior (AI): es el ángulo formado, internamente al polígono, por dos lados consecutivos.
*Ángulo exterior (AE): es el ángulo formado, externamente al polígono, por un lado y la prolongación de un lado consecutivo.

*En un polígono regular se puede distinguir, además:
*Centro (C): es el punto equidistante de todos los vértices y lados.
*Ángulo central (AC): es el formado por dos segmentos de recta que parten del centro a los extremos de un lado.
*Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
__________________________________________________
"n" es el número de lados
Ángulo central
Ángulo central = 360°/n
Ejemplo 360°/6= 60°

Ángulos interiores
i= (n-2)(180°)n
Ejemplo i=(6-2)(180)
6
i=(4)(180°)
6
6
i=(4)(180°)
6
i= 720
6
i=120
Suma de ángulos interiores
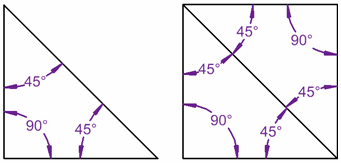
(n-2)(180°)
ejemplo:
SI=(4-2)(180°)
SI= 2x 180
Si=360

 .........................................................................................................
.........................................................................................................
Es la linea curva que delimita un área en el espacio denominada círculo
La circunferencia posee lugares geometricos donde se pueden formar ángulos llamadas "rectas o segmentos

ÁNGULO CENTRAL

Es el ángulo que tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.

6
i=120
Suma de ángulos interiores

(n-2)(180°)
ejemplo:
SI=(4-2)(180°)
SI= 2x 180
Si=360
Suma de ángulos exteriores
360
n

Ejemplo:
e= 360°
3
3
e=120°

LA CIRCUNFERENCIA
Es la linea curva que delimita un área en el espacio denominada círculo
La circunferencia posee lugares geometricos donde se pueden formar ángulos llamadas "rectas o segmentos

ÁNGULO CENTRAL

Es el ángulo que tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.

 El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella. 
 El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella. 
 Su vértice es interior a la circunferencia y sus lados secantes a ella. a.
Su vértice es interior a la circunferencia y sus lados secantes a ella. a.
 Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella.
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella.



No hay comentarios:
Publicar un comentario